グーグルの囲碁AI「AlphaGo(アルファ碁)」は囲碁の謎をどのように解いたのか?(モンテカルロ法とディープラーニングについて)(追記あり)

15年10月、同社のロンドンオフィスで人間対コンピューターの試合が行われた。そこでは「AlphaGo」と呼ばれる囲碁ソフトが現欧州チャンピオンである樊麾(ファン・フイ)との対局に臨み、英国囲碁協会からの立会人と学術誌『Nature』のシニアエディターであるタンギ・シュアール博士が見守るなか、5局すべてでチャンピオンを倒したのだ。
欧州の棋界のレベルは東アジアにまだ及ばず、欧州チャンプはレベル的にはこちらのトップアマレベル、という声もある。ただ、ここまで来ればもはや(ほぼ近い将来の運命が確定したという意味で)時間の問題だろう。
(2016.3.11追記 ここ10年で世界最強と名高いイ・セドルを撃破。早えーよ。)
今回のニュースのポイントは、AIの方式を力ずくの選択肢ツリー総当り法式からモンテカルロ木探索とディープラーニングの組み合わせに換えたことで、マシンパワー×制限時間の範囲内でより有効な手が選択できるようになったということにある。
モンテカルロ木探索とは何か?
まずはその原型であるモンテカルロ法について。
モンテカルロ法とは、簡単に言えば「乱数に基づく試行を繰り返し、その結果を統計的に読み解くことで、求めるものについての近似解を導く」という方法論だ。
例えば円周率πの値を求めたいというとき。
下のような、一辺の長さが2aの正方形と直径が2aの円を重ねあわせた図形を用意する。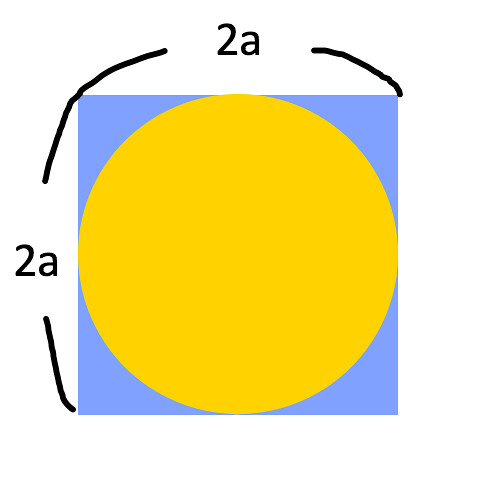
このとき正方形の面積は4a^2、円の面積はπa^2となる。
この図形の中にランダムに点を落とし、その点が円の内部(黄色いエリア)に落ちたか、円の外部(青いエリア)に落ちたかの結果を記録していく。
点の位置は完全にランダムなので、黄/青どちらのエリアに点が落ちるかという比率は、それぞれのエリアの面積比に等しい。
たとえば5回の試行の結果、「黄」対「青」が1:4だったとする。
そうすると、
4a^2-πa^2:πa^2=1:4
という推定が成り立つ。式を解くと
πa^2=16a^2-4πa^2
⇔ 5πa^2=16a^2
⇔ 5π=16(∵a>0)
⇔ π=16/5
ということで、πは16/5=3.2くらいじゃねーかという推定ができることになる。
5回程度の試行だとかなり大雑把な推定しかできないが(上記のパターンはむしろ点が上手く落ちてくれたほう)、試行回数を増やすほど、正確な値に近い推定が可能となる。
モンテカルロ法は、限られた試行回数の中で近似の解を出すことに優れる。いわば、あるだけものでそれなりの答えを出す、という手法になる。
なので、囲碁プログラムに用いるのなら、持ち時間いっぱいの中である程度有効な手を導ける、ということだろう。
ただしモンテカルロ法には弱点がある。
モンテカルロ法で足りないところ ――囲碁は手数が多く、そして頭の切れる対戦相手がいる
上の円周率の値を求める問題では、
- 「点打がどちらのエリアに入るかの比率」と「面積比」が等しいこと
- 円の面積と円周率の関係が明らかになっていること
の2つが前提にある。
「囲碁を打って勝つ」というプログラムでこれを考えるなら、モンテカルロ法を適用するためには「どういう手が優れた手なのか否か」(=「この図形と点から何を読み取ればいいのか?」)という基準が必要となる。だが、モンテカルロ法自体はこの基準を自ら定めてはくれない。
「どういう手が優れた手なのか否か」という基準、これを評価関数と呼ぶ。
囲碁の評価関数は難しい(πに関する諸法則がこの上なく明らかなのとは対照的だ)。チェスや将棋より囲碁がAIにとって難解となる要因はここにある。碁石には駒のように点数差を付けることができず、勝敗の判断基準が盤面の形勢そのものしか存在しないからだ。
評価関数を上手く設定できずとも、マシンパワーが囲碁の全手筋をシミュレートできるほどあれば話は早い。相手がどう打っても勝つ必勝手を見つけられれば終わる。
だがここに囲碁の難解さがある。囲碁の可能な手数は10^360~700手と言われている。これは現在観測可能な宇宙の原子の数(約10^80)より多い。全パターンを打ち切ることはできない。
そこでモンテカルロ法の出番なのだが、局面に対する評価関数がない以上、唯一評価できるものは勝敗のみ。なので、可能な次の手それぞれについて「ランダムに石を配置し続けて終局まで打ち切る」という試行(これはプレイアウトと呼ばれる)を同数回マシンパワーの許すだけ行い、一番勝ちのプレイアウトが多かった手を次の手として採用することになる。
勝敗以外に評価関数を持たないこのような試行法を原始モンテカルロ法と呼ぶ。
原始モンテカルロ法は、しかし、弱い。
- その後も完全にランダムに打ち続けたとき勝率5割となる一手
- その後も完全にランダムに打ち続けたとき勝率2割となる一手。但しそのうちある手筋を選ぶと勝率7割となる
原始モンテカルロ法は二手のうち前者を選ぶ。しかし局面を評価する能力を持つ相手は、その能力の限りで後者の中の勝率7割の道を選ぶことができるのだ。(これは人間から見ると、ソフトが対戦相手のしょうもないミスを期待しているように見える)
原始モンテカルロ法をもう少しどーにかできんか、ということで改良された新たなアルゴリズムがモンテカルロ木探索である。
モンテカルロ木探索 ――立ち止まって反省しよう
モンテカルロ木探索の肝は次の3つ。
- どの手が有利そうか、信頼上限(UCB)の大きさで判断する
- 有利そうな手により多くのプレイアウトを割り当てる
- 割り当てられたプレイアウト数がある閾値を越えたらそこから枝を展開する(次の手ではなく次の次の手をプレイアウトの対象とする)
信頼上限(UCB)とは?
簡単にいえば、その手の有利さを確率的に判断して点数化したものである。
たとえば、囲碁のある局面で、
- 次の打てる手はa、b、cの3通り
- マシンパワーと時間制限の範囲内で、10,000回のプレイアウトが可能
とする。
原始モンテカルロ法ではa、b、cをそれぞれ3,333回プレイアウトした結果で手を選択するのだが、その前に、それぞれの手を100回プレイアウトした時点でいったん統計を取る。仮にa、b、cの勝率が70%、50%、30%だったとしたら、aの試行の信頼上限が最も大きく、cのそれが最も小さくなる。
こうなると、以降の9,700回の試行はa>b>cというように傾斜配分したほうが資源の有効活用になりそうだ。ということで次のプレイアウト100回(400回目まで)はa:50回、b:35回、c:15回と傾斜配分して行うことにしよう。
その結果、
- a:62%(試行回数150回)
- b:56%(試行回数135回)
- c:29%(試行回数115回)
となったとする。
こうなると、以降の試行は今回よりa、cに賭ける配分を薄くし、bを厚くしたほうが良さそうだ。ということで……
というように、信頼上限を用いることで、浅い読みの段階でどの手をより深く読んでいくかを選びとることができる(ちなみに実際の信頼上限値の求め方はもっと複雑)。
また、ある一手へのプレイアウト数の配分が特定の閾値を超えたときには、そこから枝を展開する。たとえばaの手の次に4通りの可能な手(α、β、γ、δ)があるとすれば、以降はaα、aβ、aγ、aδ、b、cに対してプレイアウトを割り当てていくのだ。
これによって、より有望な手筋へより多くの計算資源を振り向けることができる。
が、まだ足りない。
モンテカルロ木探索でまだ足りないところ ――囲碁にはなぜ定石があるのか
信頼上限以外にある一手の有望さを判断する材料はないだろうか?
ある。定石である。
その場で確率を求めるまでもなく、明らかに筋が良い/悪い手が存在する。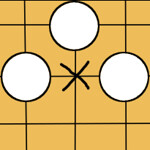 _
_
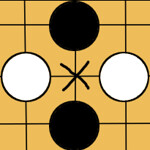
自分が黒で次手のとき、上左図の×に打つのは多くの場合で悪手であり、右図は良手である。
ある手の良否は統計的に判断することができる。囲碁の全局面をシミュレートできないのなら、上図のように3×3に盤面を区切ればいい。この3×3の世界での良否は、資源配分を傾斜させる際の判断材料になるはずだ。これを人の手でプログラムに組み込めばよい。盤端でのやりとりが盤上のそれ以外の場所と異なることも考慮に入れよう。
また、碁盤は天元を中心として点対称であり、かつ天元を通る2直線で線対称でもあることから、対称性を考慮することで試行回数を削ることができる。鏡写しにして同じ配置になる手なら、その有望さも同じである。これもプログラムに入れておこう。
このように、モンテカルロ木探索を囲碁の知識でサポートする(Progressive Widening)ことで、以前とは比べ物にならない強さの囲碁ソフトたちが誕生した。
代表例であるレミ・クーロンのCrazyStoneは2013年と14年、4子のハンデで日本のプロ棋士2名に勝利した。
だがこれらのプログラムは、いまだに人の力を借りているままだ。効率的な試行のためには、どうしても局面を評価することが必要だ。
コンピュータに囲碁の盤面を評価させるには?
特徴量 ――この1手の盤面における意味とは?
目の前にある情報について、ある部分を他の部分から際立たせるものを「特徴」と呼ぶ(ほかに属性、素性といった呼び方もあるようだ)。この「特徴」は、人間があるモノとそれ以外を区別する際にその手がかりとしているものでもある。
たとえば犬について考えてみよう。
- 前足と後ろ足を2本ずつ持ち、全身を毛で覆われており、尾があり、目・耳・鼻・口を一般的な哺乳類と同じ数そなえ、目はどちらかというと黒目がちで、鳴き声は「ワン」とか「BOW WOW」と聞こえ、足の爪は基本的に出ていて、人に比較的懐きやすい動物
- アザトースを筆頭とする外なる神に使役されるメッセンジャーでありながら、旧支配者の最強のものと同等の力を有する土の精であり、顔がない故に千もの異なる顕現を持ち、特定の眷属を持たず、狂気と混乱をもたらすために自ら暗躍する旧支配者の一柱
上に挙げた2者のうち、犬であろうと推測されるのは前者だろう。
「前足と後ろ足を2本ずつ持ち」だとか「全身を毛で覆われており」だとかが、特徴である。目の前のさまざまなデータから対象を判断/評価/位置づけするために特徴は用いられる。
だが、眼前のデータから得られる特徴すべてが対象の判定に有用なわけではない。前者の説明文にはあらかじめ、「黄土色の毛並だった」「右目のまつげの方が本数が多かった」「尾の長さが6cm未満だった」あるいは「それを観察していた際に飛行機が上空を飛んでいた」「寒かった」「議員が不倫スキャンダルで辞職した」「トイレシートからいつも尿が漏れる」等の情報が省かれていた。
実際得られていてもおかしくないこれらの情報が省かれていたのは、筆者がこれらを、対象が犬であるかどうかの判定において有用性が低い情報だと判断したからである。
この判断は、特徴選択と呼ばれている。特徴選択によって、判断を行う者は、不要な検討を省き、高速な判断処理が可能となる。
これまでの機械学習では、データのどの部分を特徴として抽出するか、また抽出した特徴のうちいずれを有用なものと判断するかは人の手によるものだった(駒にそのパワーに応じた点数をつけたり、ある局面に点数をつけたり)。
ディープラーニングの登場
ここに、ディープラーニングという新しい方法が登場した。ディープラーニングの革新性は、特徴の抽出と選択が自動で可能だというところにある。
モンテカルロ法を適用するために必要だった「どういう手が優れた手なのか否か」という特徴=判断基準を、ディープラーニングによって、AIが自ら発見してくれるのだ。
AlphaGoの場合、碁盤上の状況を評価する「value networks(状態価値関数ネットワーク)」と、個々の手を評価する「policy networks(教師あり方策ネットワーク)」という2つのプロセスがディープラーニングを用いて運用されている。
ディープラーニングが「有効な1手とはどのような手か」という判断基準を提供し、モンテカルロ法でその近似解を計算資源の限りを尽くして求める、という組み合わせが、囲碁AIのブレークスルーをもたらしたのだ。
なぜディープラーニングが注目されるのか ――AIが意味を理解する?
ディープラーニングの確立によって人工知能(AI)界隈がにわかに盛り上がった理由は、ディープラーニングの上記のような機能のためだ。犬の話を再び持ちだすと、犬の特徴を抽出し、選択することで浮かび上がるものは何の輪郭だろうか? そこで現れるのは、「犬」という概念=意味である。実際に、googleのAIは世界から猫を発見した。
AIはYouTubeから猫を発見し(具体物の一般概念)、碁盤の上で勝ち筋を見つけられるようになった(ルール、法則、定石という方法の概念)。
意識、感情、飢え、そして愛といった概念を彼らが理解する(あるいは、それらが我々が思っていたようなものではなかったことを暴く)のはいつごろになるだろうか。
(2016.03.11追記)モンテカルロ木探索についての記述を追加。
